简介
之所以要做这么一件事情是因为在玩《Cities: Skylines》时,游戏内的立交建造比较繁琐,又很重要。于是就萌生了做一个从目前已有的二维地图道路数据自动生成立体的立交道路的工具的想法。
以延安东路立交桥为例,第一张是平面展示效果,第二张是立体展示效果:
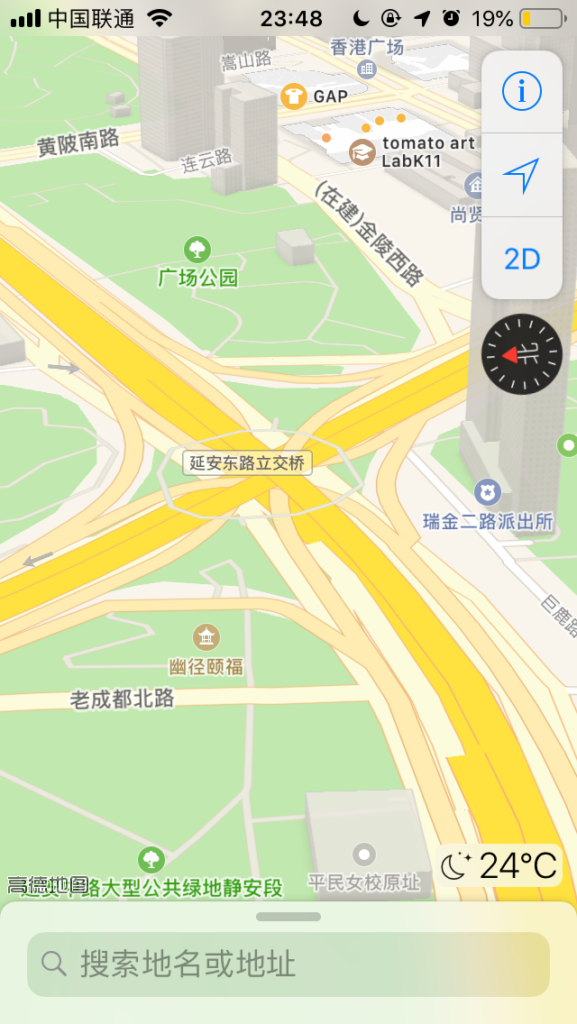
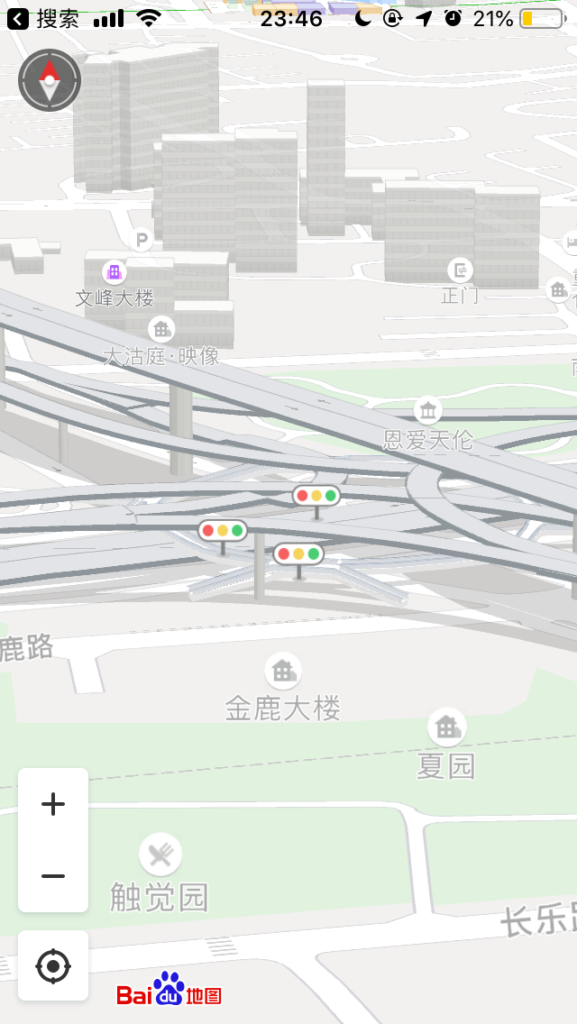
如果能用第二张图中的道路数据,导入到游戏中,想必很实用。所以,接下来的内容就是介绍我的想法,关于如何从图一中的数据计算得到图二中的数据。
计算原理
道路在平面上的坐标是已知的,但是要如何才能把道路在垂直方向上的坐标计算出来呢?或者说,道路的哪些属性能够帮助到我们?
如果在 OSM 上编辑过复杂一点的道路数据的话,可能会注意到一个属性,用来体现道路之间的压盖层级的。
- 例1:东西方向的A路为高架路,南北方向的B路为普通地面道路,则A路的层级比B路高。
- 例2:东西方向的C路为地下隧道,南北方向的D路为普通地面道路,则C路的层级比D路低。
这个压盖层级在在 OSM 编辑地图数据的时候,使用的名称为“Layer”,进入到后台数据库后则体现到了“z_order”这个字段上。这个属性的最直接的意义就在于,渲染地图的时候, 渲染引擎能够知道同一位置上叠加的道路的渲染顺序。
既然已经能够知道道路在垂直方向上的排列顺序,那么,再结合一些额外的信息,是可以计算得到道路上的一个节点的高度值的,或者至少说是一个节点的取值范围。
这里的额外信息,指的是以下这些:
- 上下相邻的两条道路高度差存在一个最小值,假设为4米。
- 一条道路上的相邻的2个节点之间的坡度值小于一个定值,假设为6%。
- 属性为地面类型的,高度固定为0米。
- 属性为高架类型的,高度至少为4米。
还要有一个假设:
- 立交桥所处的范围内的地面高度都为0米,不考虑地势对道路的影响。
根据以上的条件,把每条道路上的每个点的高度值作为一个未知数,可以列出一个不等式方程组。
那问题又来了,怎么解?好像解不了。那就还要再引入一个假设:
- 组成立交的每一条道路都尽可能的低,为了减少造价。
上面的这个假设实际上是一个目标函数。于是,问题就变成了,有了约束条件, 求目标函数的最优解,一个普通的线性规划问题。
数据准备
数据获取
OSM 的数据可以很方便的下载到,这里不再赘述。我分别选取了上海,约翰内斯堡,西雅图这三个城市的各一座立交桥作为测试数据。(实际上最终只在上海的延安东路立交桥和莘庄立交上做了尝试)

数据加工
单次计算只针对一个立交桥,并且不涉及除立交道路以外的道路,例如立交下的普通的城市道路。所以需要对数据进行筛选并提取。
按道路属性进行筛选的时候需要注意,高速公路的道路类型和城市快速路的类型可能会不一样。
数据命名
对道路的高度值的计算,实际上是计算道路上各个点的高度值。为了方便计算,需要把道路上的点分为4类:
- 交叉点(Cross Point):简称
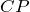 。两条不同的道路,在正视时形成的交叉点,但实际上因为两条道路高度必然不一样,实际中并没有相交。这样同一个交叉点最终对应了2个需要计算的未知数,分别对应两条不同的道路。
。两条不同的道路,在正视时形成的交叉点,但实际上因为两条道路高度必然不一样,实际中并没有相交。这样同一个交叉点最终对应了2个需要计算的未知数,分别对应两条不同的道路。 - 接触点(Touch Point):简称
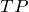 。匝道与主道进行合并时形成的点,一个接触点实际上对应了2条道路。
。匝道与主道进行合并时形成的点,一个接触点实际上对应了2条道路。 - 终点(End Point):简称
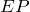 。道路两端的点。
。道路两端的点。 - 普通点(Normal Point):简称
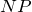 。除了以上三种类型以外的点。
。除了以上三种类型以外的点。
最终需要计算的是前3类点,第四类点可以在线性规划完成后通过插值来计算。
算法实现
空间关系
所有提到的涉及到空间关系的计算方式,均由PostGIS完成。此处不是文章的重点,不细说,详情请参考文档“https://postgis.net/docs/manual-2.4/”。仅罗列一下部分用到的函数。
- 计算道路交叉点:ST_Intersection()
- 去除重复点:ST_Removerepeatedpoints()(由于精度问题,需要用PostGIS的函数来实现,而不是SQL)
- 合并多条线:ST_LineMerge()
- 判断要素是否有公共点:ST_Touches()
约束条件
下面的公式写的可能不规范,如有错误请指出。
- 根据道路属性,如果是地面道路则高度衡定为0,如果是高架道路,则高度大于等于3。暂不考虑隧道类型的道路。
![Rendered by QuickLaTeX.com \[\begin{cases} Height(P_i) = 0, & Type(road_i) = Bridge \\ Height(P_i) >= 3, & Type(road_i) <> Bridge \end{cases}\]](https://littlepotato.me/wp-content/ql-cache/quicklatex.com-7ef25334def44480b990c34ac594d979_l3.png)
- 两点之间的坡度要小于等于指定值,注意,这里的
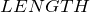 指的并不是两点之间的直线距离,二是沿道路前进曲线的距离。
指的并不是两点之间的直线距离,二是沿道路前进曲线的距离。
![]()
- 上文提到的两条不同高度的道路在正视时会存在交叉点,这个交叉点实际上是2个点,平面坐标是一样的,但是高度不一样。根据道路的“z_order”属性,可以知道这两个点,哪个在上,哪个在下。
![]()
目标函数
目标就是“组成立交的每一条道路都尽可能的低,为了减少造价”。所以需要使得道路的线数据中所有点的高度值之和最小:
![Rendered by QuickLaTeX.com \[S=\sum_{i=1}^m\Height(CP_m)+\sum_{i=1}^n\Height(TP_n)+\sum_{i=1}^p\Height(EP_p)+\sum_{i=1}^q\Height(NP_q)\]](https://littlepotato.me/wp-content/ql-cache/quicklatex.com-506537e590285f6dfc4c8436bffb7fd2_l3.png)
线性规划求解
求解线性规划使用了 Google 的 ortools 库,参考文档链接:Linear Optimization,以下的代码中的英文注释是文档里的,我就不翻译了,免得不达意而引起误解。
创建一个解决线性规划问题的对象:
from ortools.linear_solver import linear_solver_pb2, pywraplp
# Create the linear solver with the GLOP backend.
solver = pywraplp.Solver('road_3D', pywraplp.Solver.GLOP_LINEAR_PROGRAMMING)
定义变量,并可以在初始化时就指定变量的取值范围:
for _n in range(0, len(cross_points)):
cp_list.append(solver.NumVar(0, solver.infinity(), 'cp_{id:02d}'.format(id=_n)))
for _n in range(0, len(touch_points)):
tp_list.append(solver.NumVar(0, solver.infinity(), 'tp_{id:02d}'.format(id=_n)))
for _n in range(0, len(end_points)):
ep_list.append(solver.NumVar(0, solver.infinity(), 'ep_{id:02d}'.format(id=_n)))
实现上述的约束条件的表达,以“两点之间的坡度要小于等于指定值”为例:
constraint = solver.Constraint(-distance * MAX_SLOPE, distance * MAX_SLOPE) constraint.SetCoefficient(cp_list[m], 1) constraint.SetCoefficient(cp_list[n], -1)
声明目标函数的对象,并设置为求最小值:
objective = solver.Objective()
objective.SetMinimization()
for _n in range(0, len(cross_points)):
objective.SetCoefficient(cp_list[_n], 1)
for _n in range(0, len(touch_points)):
objective.SetCoefficient(tp_list[_n], 1)
for _n in range(0, len(end_points)):
objective.SetCoefficient(ep_list[_n], 1)
求解:
solver.Solve() # 输出一个求解结果 print(cp_list[_n].solution_value())
“异常下降”
这样的模型实际上是存在一个问题的,假设在一条道路上选取连续的3个点,分别为A,B,C,点A和点C的下方因为存在道路,所以高度最终计算得到为4米,点B的下方没有道路,那么点B的高度为多少?
按照常识,点B的高度应该也是4米。但是按照上面的模型,点B会在坡度限制范围内尽可能的低,那么实际生成出来的道路就会呈现出一个异常的下降,根据我朴素的日常经验来看,这是不应该的。
目前的做法就是在线性规划计算完成后,再对数据进行一遍检查,弥补这样的问题。
结果预览
在上面求出结果之后,还需要有一些后续的处理流程,比如整合,插值,按指定格式输出等。目前是将数据保存到 PostgreSQL 数据库中,并输出为kml格式的文件,方便在 Google Earth 中查看。
存在的问题
- 存在个别点
 值计算错误的问题。引起这个问题的原因有几个,一个是上面提到的“异常下降”的问题;二是并非所有的立交都会遵守程序所设定的最小高度差和最大坡度;也不排除程序本身存在bug,会使得一些点的
值计算错误的问题。引起这个问题的原因有几个,一个是上面提到的“异常下降”的问题;二是并非所有的立交都会遵守程序所设定的最小高度差和最大坡度;也不排除程序本身存在bug,会使得一些点的 值为0。
值为0。 - 所有的计算都是基于地面为平面进行的,然而在实际生活中并不完全是这样。
- 因为不清楚《Cities: Skylines》中的数据规格,所以无法把已有的数据导入到游戏中。
因为懒,这些问题还没有解决。

膜拜大佬!!天际线2有从游戏导出路网的模组,并且导出的模组可以在qgis中进行最短路径查询等操作,所以应该存在一套天际线格式到GIS格式的对应方案,理论上可以将现实路网导入。
后面可以试试,不过现在天际线2的资产模组啥的还不太完善。