deck.gl 是一个开源的 WebGL 驱动框架,用于对大型数据集进行可视化的探索性数据分析。因为工作需要,我尝试改造 deck.gl 以让它支持 EPSG:4326 投影坐标系。最终实现代码可以参考:deck.gl with EPSG:4326。不过,在我改造代码的过程中,发现在 deck.gl 源码里有这样的一段:
get projectionMode() {
if (this.isGeospatial) {
// I modified
return PROJECTION_MODE.WEB_MERCATOR;
// deck.gl source code
// return this.zoom < 12
// ? PROJECTION_MODE.WEB_MERCATOR
// : PROJECTION_MODE.WEB_MERCATOR_AUTO_OFFSET;
}
return PROJECTION_MODE.IDENTITY;
}
在地图层级大于等于12级时,全局的投影参数会从 WEB_MERCATOR 转换为 WEB_MERCATOR_AUTO_OFFSET。实际上这里的 WEB_MERCATOR_AUTO_OFFSET 即 deck.gl 的“地平”模式。“地平”模式将地理空间可视化的渲染性能提升最多 48 倍。本文将深入介绍其工作原理。
在着色器中实现 Web Mercator 投影的挑战
在运行时,deck.gl 的 MapView 使用 Web Mercator 投影将地理特征显示在屏幕上。在渲染每一帧时,根据用户交互设置的缩放级别,deck.gl 对每个坐标执行以下转换,将 [经度,纬度,海拔] 转换为 Mercator 平面上的 [X,Y]:
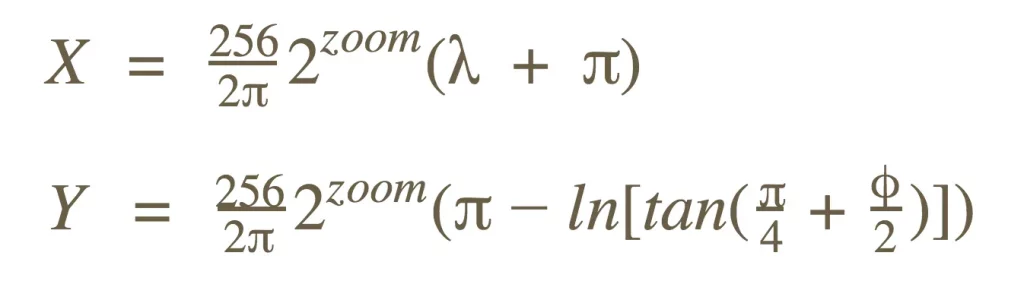
正如你所看到的,从纬度到 Y 的映射是非线性的。这个计算依赖于昂贵的三角函数和对数运算,并且必须针对每个坐标在可能非常大的数据集中执行。这是因为地球不是平的!

与大多数地图库(如 Mapbox GL JS)不同,deck.gl 并不在 CPU 上进行处理。因为 deck.gl 旨在处理大量频繁变化的数据点,在 CPU 上进行 Web Mercator 投影会导致严重的性能损失。相反,它将坐标原样传递给 GPU,并在顶点着色器中执行这些转换。
当我们将地理位置传递到 WebGL 着色器时,出现了一个新问题。根据 WebGL 参考卡,浮点数的精度如下:
| FP Range | FP Mangitude Range | FP Precision | Integer Range | |
| highp | (-262, 262) | (2-62, 262) | Relative 2-16 | (-216, 216) |
| mediupm | (-214, 214) | (2-14, 214) | Relative 2-10 | (-210, 210) |
| lowp | (-2, 2) | (2-8, 2) | Absolute 2-8 | (-28, 28) |
考虑以下位置:[-122.4000588, 37.7900699]。将其转换为 32 位浮点数后,我们得到 [-122.40006256103516, 37.790069580078125]。这两个点之间的实际差异是 0.3325 米。
其结果是,当进行大范围概览时,一切正常,但在放大时,精度问题开始显现,点会明显变形并在视口发生最轻微变化时“跳动”。
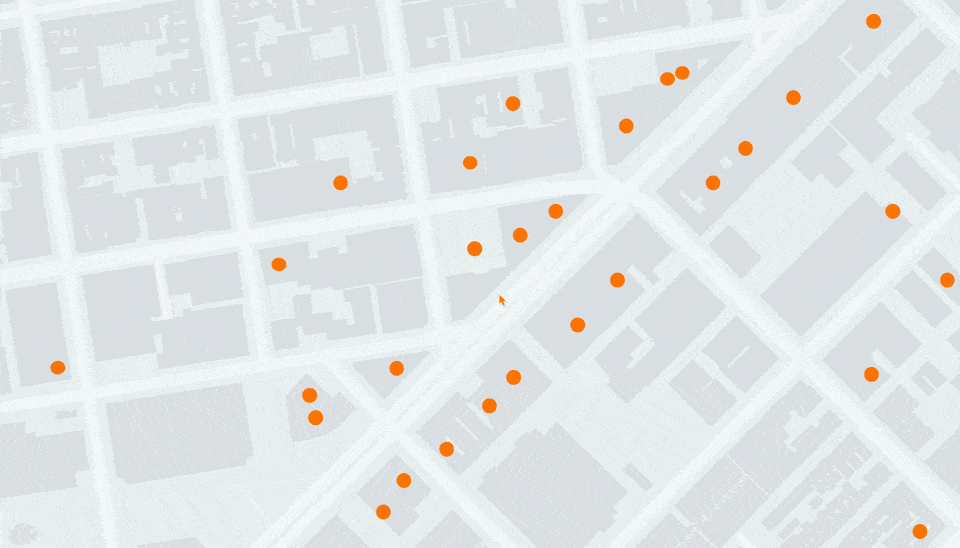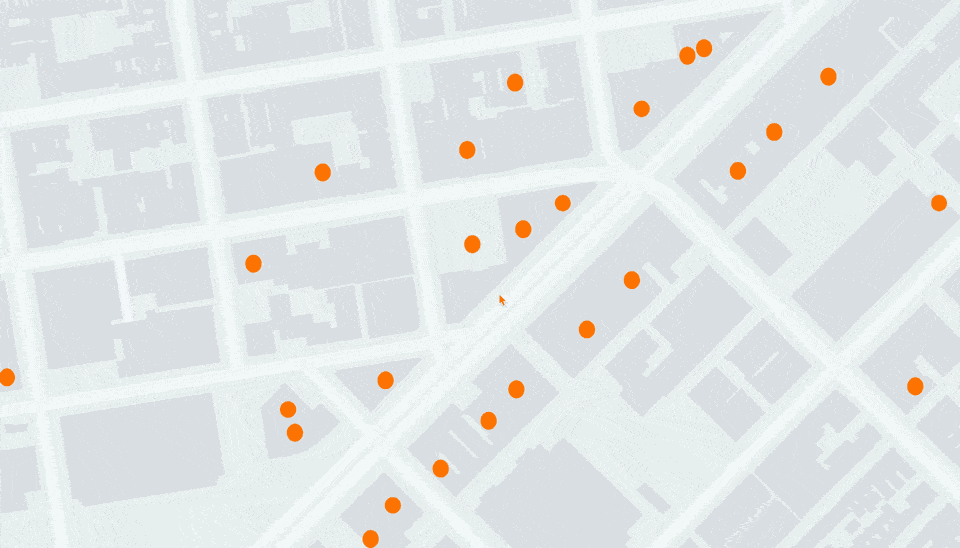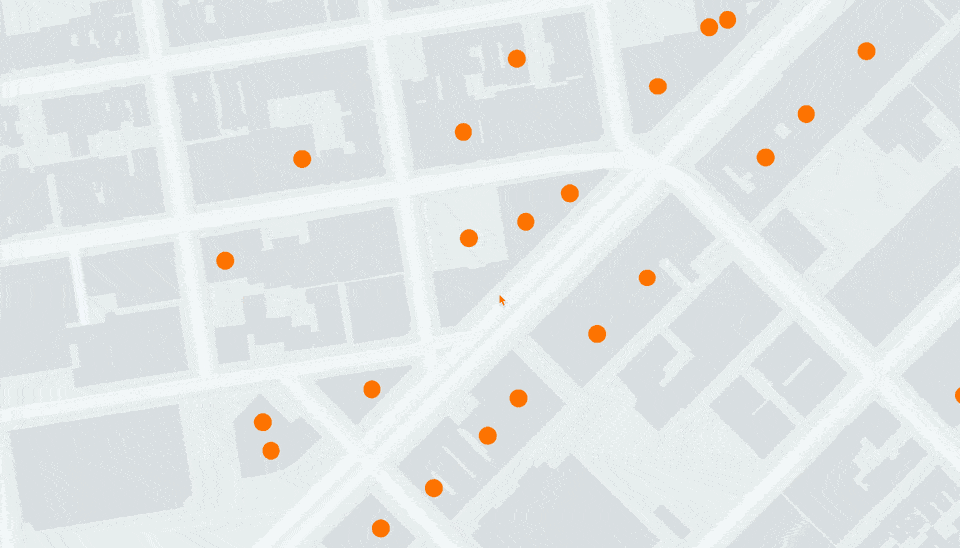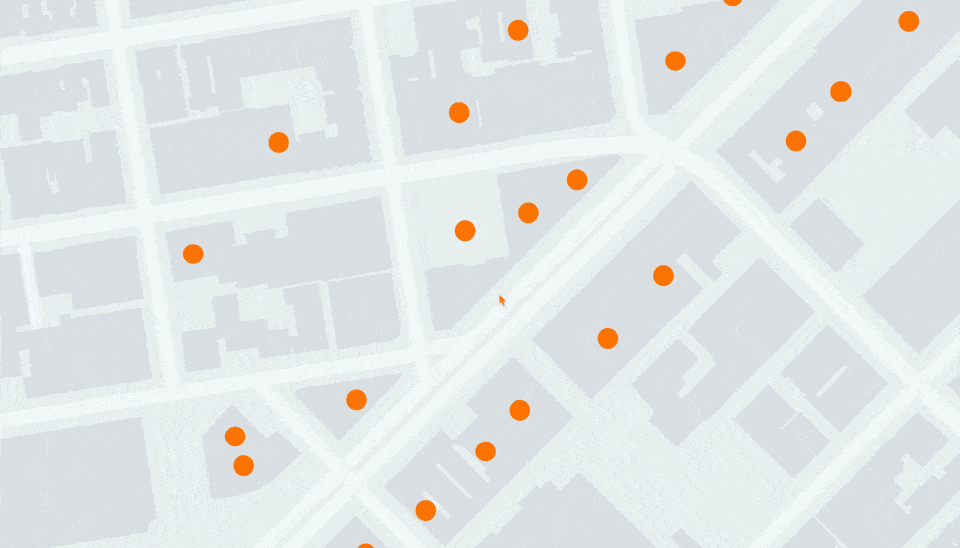
引入模拟的64位浮点数
为了减少这个问题,deck.gl v3 引入了模拟的64位精度浮点数。每个数字被分成两部分发送到GPU:
highPart = Math.fround(x)
lowPart = x – highPart
然后,我们通过一系列操作使用32位浮点数来模拟64位浮点运算,这会消耗更多的GPU计算周期。例如,一个64位的除法操作将映射到11个32位的算术操作,而一个64位的mat4到vec4的乘法则需要1952个32位的操作。该算法的具体细节超出了本文的范围,但如果你感兴趣,实际的代码可以在 luma.gl 中找到。
尽管模拟的64位矩阵运算几乎能提供完美的结果,但它会严重影响运行时性能。由于着色器代码体积庞大,一些较旧的显卡驱动程序无法兼容,而其他一些驱动程序则需要数秒钟才能编译代码,导致浏览器出现卡顿现象。
替代解决方案:offset 模式
作为 emulated fp64 解决方案的更便宜替代方案,deck.gl v5 引入了 LNGLAT_OFFSETS 坐标系统。在此模式下,代替使用 [lng, lat],每个地理位置使用 [Δlng, Δlat] 来表示相对于固定点(坐标原点)的“偏移”。在着色器中,使用线性近似将经纬度差转换为 Mercator 平面上的像素差:
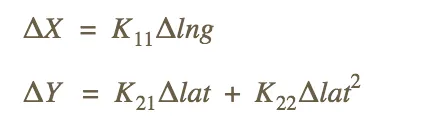
其中,常数 K[ij] 是通过使用二阶泰勒级数展开,根据坐标原点的纬度来确定的。
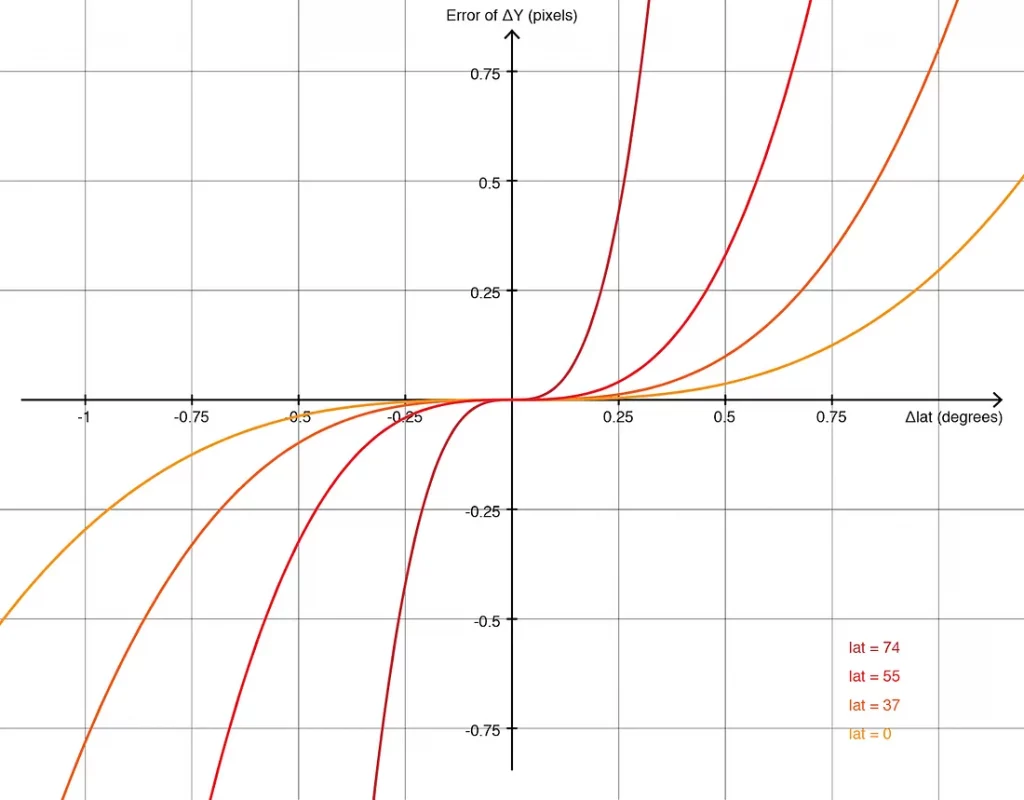
虽然线性近似的误差随着偏移量的增加而增大,但在±0.1度的范围内(足够覆盖一个城市的范围),误差通常是无法察觉的。在局部范围内,我们可以假设地球是平的。当偏移量如此小的时候,32位浮点数足以捕捉所需的精度,从而消除了对复杂的仿真64位运算的需求。由于不涉及三角函数,着色器的执行速度极快。
然而,使用这种坐标系也有显著的缺点。首先,用户需要编写额外的代码来从原始数据中提取偏移量。此外,任何预定的坐标原点只能确保在有限地理区域内的误差是可接受的。在处理大范围的数据集时,可能需要进行预先的切片处理。
另外一个主意
在处理高负载、对精度敏感的地图应用时,我们常常希望能够同时拥有两者的优势:传统的 LNGLAT 坐标系统的便利性,以及 LNGLAT_OFFSETS 坐标系统的高性能。这个想法很简单:不再指定固定的坐标原点,而是将所有坐标转换为从视口中心开始的“偏移量”,并在 GPU 上进行处理。
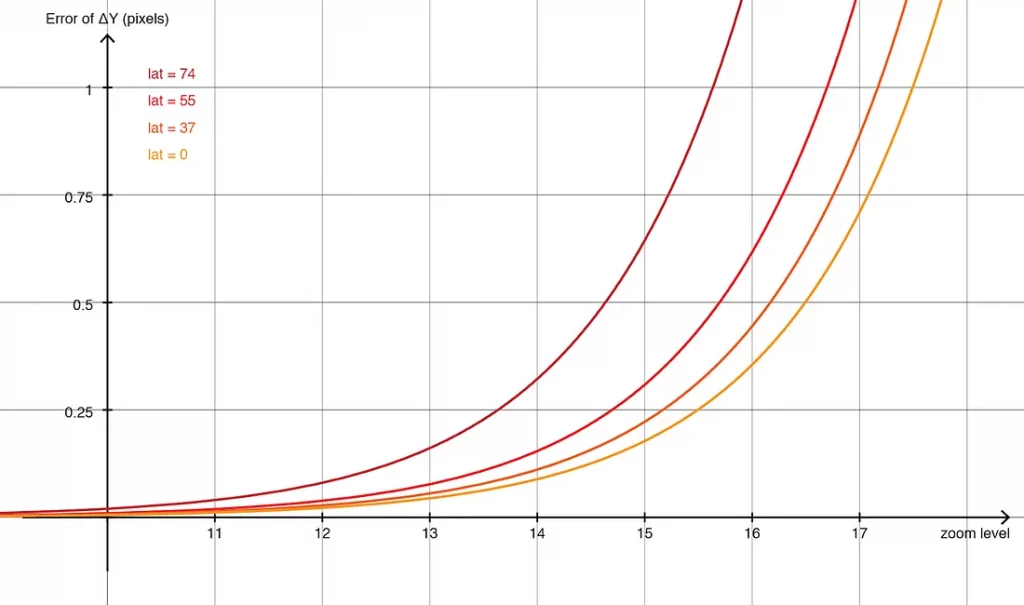
动态选择坐标原点对我们有利:视口的大小是有限的,这意味着任何远离中心的点在投影时出现较大误差的情况,会被屏幕边缘裁剪掉。更好的是,随着缩放级别的增加,视口的覆盖范围呈指数级缩小,从而抵消了误差的比例效应。
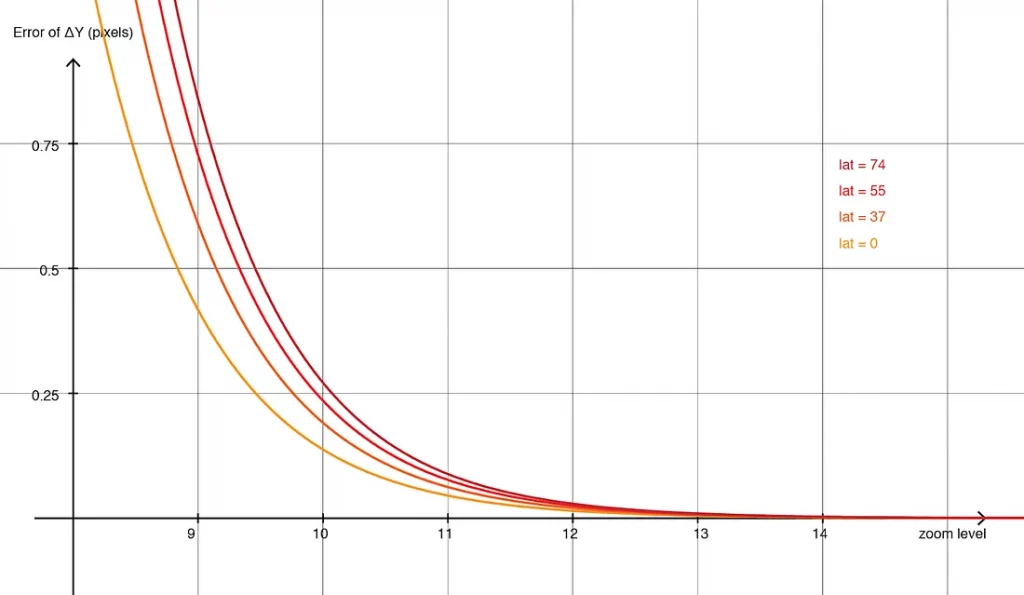
将此图与 32 位 Web Mercator 投影的图表进行比较,我们创建了一种新的坐标系统,结合了正常模式和自动偏移模式:当缩放级别低于某个阈值时,我们将使用“正常”投影;否则,我们将使用坐标偏移的“平面”模式,将中心点设置为视口的中心。我们始终在任何给定的缩放级别选择误差较小的模式。
在每一帧,deck.gl 会比较缩放级别并相应地更改投影方法。切换投影模式只需要更新少量的 uniform 变量,几乎不会对 CPU 或 GPU 时间产生任何成本。
总结
精度
新的混合坐标系统(黄色)与 64 位模式(红色)具有可比的准确性,尽管它仅使用 32 位。而传统的 32 位模式(蓝色)在相同的缩放级别下不稳定。

性能
新的混合坐标系统比旧的 32 位模式更快,比旧的 64 位模式快最多 48 倍。
| Mode | Zoom Level | FPS | Compare with 64-bit |
| 64-bit | 11 | 1.9 | 1X |
| Legacy 32-bit | 11 | 16.4 | 9X |
| New 32-bit | 11 | 15.7 | 8X |
| 64-bit | 14 | 1.9 | 1X |
| Legacy 32-bit | 14 | 59.5 | 31X |
| New 32-bit | 14 | 91.7 | 48X |
