简介
分词工具也算是接触过一点了,目前工作上主要用到的一个是MMSEG,另一个是jieba分词。对于分词,可不能就简单的调调接口,所以现在就来看一看分词算法的相关原理,并尝试实现一个简单的分词工具。
算法原理
MMSEG
MMSEG基于字符串匹配,即扫描字符串,使用如正向/逆向最大匹配,最小切分等策略,也就是基于词典。具体使用的时候,通常是多种算法合用,或者一种为主、多种为辅,同时还会加入词性、词频等属性来辅助处理(运用某些简单的数学模型)。
MMSEG的主要思想是每次从一个完整的句子里,按照从左向右的顺序,识别出多种不同的3个词的组合,然后根据下面的4条消歧规则,确定最佳的备选词组合。
- 备选词组合的长度之和最大
- 备选词组合的平均词长最大
- 备选词组合的词长变化最小
- 备选词组合中,单字词的出现频率统计值最高
正向最大匹配
对输入的句子从左至右,以贪心的方式切分出当前位置上长度最大的词,组不了词的字单独划开。其分词原理是:词的颗粒度越大,所能表示的含义越精确。
逆向最大匹配
原理与正向最大匹配相同,但顺序不是从首字开始,而是从末字开始,而且它使用的分词词典是逆序词典,其中每个词条都按逆序方式存放。在实际处理时,先将句子进行倒排处理,生成逆序句子,然后根据逆序词典,对逆序句子用正向最大匹配。
双向最大匹配
将正向最大匹配与逆向最大匹配组合起来,对句子使用这两种方式进行扫描切分,如果两种分词方法得到的匹配结果相同,则认为分词正确,否则,按最小集处理。
jieba分词
从项目的介绍信息来看,简单来说,分三步:
- 基于前缀词典实现高效的词图扫描,生成句子中汉字所有可能成词情况所构成的有向无环图 (DAG);
- 采用了动态规划查找最大概率路径, 找出基于词频的最大切分组合;
- 对于未登录词,采用了基于汉字成词能力的 HMM 模型,使用了 Viterbi 算法。
算法关键点
无论是 MMSEG 还是jieba分词,都免不了基于字典数据对输入句子的拆分的工作,主要的区别在于根据字典进行拆分后,如何选出合适的字词组合方式。接下来就仔细看一下jieba分词实现的各个细节。
前缀词典
不同于MMSEG中使用Trie树来存储前缀词典,jieba分词的python实现中采用的是基本的集合来存储前缀词典,项目的issue中提到过这个问题。
Trie树算法介绍:数据结构之Trie树,至于为什么Trie树的效率不如前缀词典,这个有待探讨。
生成有向无环图(DAG)
有向无环图,directed acyclic graphs,简称DAG。有向无环图的构建方式如下:
从前往后依次遍历文本的每个位置,对于位置k,首先形成一个片段,这个片段只包含位置k的字,然后就判断该片段是否在前缀词典中,
- 如果这个片段在前缀词典中,
- 如果词频大于0,就将这个位置i追加到以k为key的一个列表中;
- 如果词频等于0,如同第2章中提到的“北京大”,则表明前缀词典存在这个前缀,但是统计词典并没有这个词,继续循环;
- 如果这个片段不在前缀词典中,则表明这个片段已经超出统计词典中该词的范围,则终止循环;
- 然后该位置加1,然后就形成一个新的片段,该片段在文本的索引为[k:i+1],继续判断这个片段是否在前缀词典中。
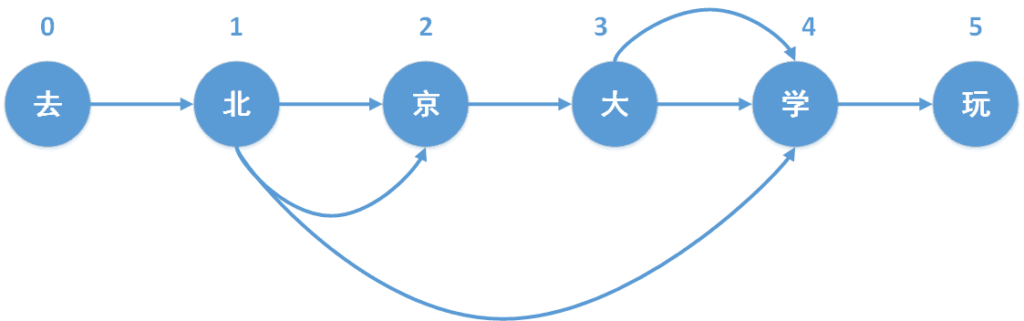
查找最大概率路径
在有向无环图中寻找最大概率路径,实际上是一个动态规划问题。这里就不多说动态规划了,可以参考这篇文章《算法笔记——动态规划》。为了求解这个动态规划问题,需要弄清楚:最优子状态与状态转移方程。
对于最大概率路径的求解,最优子状态是从起点到指定的一个节点的最大概率值。状态转移方程是:
当前节点的最大概率值 = max(当前节点前一个节点的最大概率值 + 当前节点到前一个节点的概率值)
利用HMM处理未登录词
对于一些垂直领域而言,比如地图数据,新词的增长并不会很快,通过词典分词是一种比较稳妥的手段。但是在某些领域,尤其是 UGC 占主要组成的领域,例如用户评价数据,二手商品数据,词典无法及时的覆盖到新词,会影响到分词的效果,进而影响到搜索的效果。同时,新词的发现在内容推荐方面也起到一定的作用。
HMM的内容太多,这里说不下。关于HMM的内容在文章《HMM的知识点》中进行详细的介绍。
