简介
之所以起了这个标题，是因为看了《Windows编程启示录》。为什么会看这本书呢？因为这本书和这篇文章《How does the calculator percent key work?》是同一个人。为什么会看这篇文章呢？因为前几天，网上曝光出了手机自带的计算器中的一个“bug”，无论是安卓，还是iOS，在自带的计算器软件中输入“10%+10%”，得出的结果是0.11，而非0.2。08年的这篇文章解释了这个问题。
What you first have to understand is that the percent key on those pocket calculators was not designed for mathematicians and engineers. It was designed for your everyday person doing some simple calculations. Therefore, the behavior of the key to you, an engineer, seems bizarrely counter-intuitive and even buggy. But to an everyday person, it makes perfect sense. Or at least that’s the theory.
How does the calculator percent key work?
当然，还有一种很形象的解释是：你还有10%的血，牧师跑过来，对你放了个“使目标剩余血量提升10%”的法术，于是，你的血量就变为11%了。且不论这种法术有多蠢，至少符合了这个计算器bug的模式。
如何解析算式
如何把一个常见的算式计算出结果呢，比如“1+2×(3+4)”？首先需要使用调度场算法将这样的中缀表达式转换为逆波兰表达式，再由逆波兰表达式计算出式子的值。
其实这样的处理逻辑也适用于自定义的计算语法，而不是仅限于现有的加减乘除，括号等。比如我就是要让加减的优先级高于乘除，可以通过修改上述的计算逻辑来实现。
调度场算法
为了简化问题，现在只考虑算式中包含数字，加减，百分号的情况。我把维基百科页面上算法的详细流程摘抄过来了，并去除了没涉及到的运算符的内容。
- 当还有记号可以读取时：
- 读取一个记号。
- 如果这个记号表示一个数字，那么将其添加到输出队列中。
- 如果这个记号表示一个函数，那么将其压入栈当中。
- 如果这个记号表示一个操作符，记做
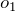，那么：
- 只要存在另一个记为
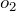的操作符位于栈的顶端，并且
- 如果 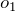是左结合性的并且它的运算符优先级要小于或者等于 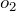的优先级，或者
- 如果 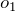是右结合性的并且它的运算符优先级比 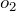的要低，那么
- 如果
- 将 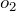从栈的顶端弹出并且放入输出队列中（循环直至以上条件不满足为止）；
- 然后，将 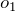压入栈的顶端。
- 只要存在另一个记为
- 当再没有记号可以读取时：
- 如果此时在栈当中还有操作符：
- 将操作符逐个弹出并放入输出队列中。
- 如果此时在栈当中还有操作符：
- 输出队列，算法结束。
逆波兰表达式求值
- while直到有输入符号
- 读入下一个符号X
- IF X是一个操作数
- 入栈
- ELSE IF X是一个操作符
- 有一个先验的表格给出该操作符需要n个参数
- IF堆栈中少于n个操作数
- （错误） 用户没有输入足够的操作数
- Else，n个操作数出栈
- 计算操作符
- 将计算所得的值入栈
- IF栈内只有一个值
- 这个值就是整个计算式的结果
- ELSE多于一个值
- （错误） 用户输入了多余的操作数
如何解析“%”
“10%+10% = 0.2”的解析方式
很方便，把“%”视为一个操作符，只需要将“%”的优先级定义为高于加减乘除，它需要1个参数 
，计算逻辑是 
。
“10%+10% = 0.11”的解析方式
假设一个场景：我买了一个100元的玩具A，又买了个200元的玩具B，玩具城的橱窗上贴着“50% off”的促销宣传，于是我掏出了手机，输入了式子“100+200-50%”，理想的计算结果是150。我用手机上的计算器试了下，确实是150。那么从代码层面要怎么实现呢？
可以将“%”的参数设置为1个或者2个，在剩余的参数大于等于2个的时候，按照“10%+10% = 0.11”的模式计算，在剩余的参数只有一个的时候，按照“10%+10% = 0.2”计算。并且，指定“%”的优先级等同于加号和减号。加减？再看一遍新宝岛。
以式子 
为例，“%” 的计算逻辑就是 
。同时，由于“%”的优先级和加减运算是一样的，对于 “100+200-50%” 这样的式子，在计算“50%”之前，会完成“100+200”的计算，然后再进行 
这样的计算。
对于乘除而言，原文当中也提到了，这里之所以不提及，是因为对于“500×5%”这样的算式，“12500”作为结果不仅违背了普通的数字计算规则，也难以在现实生活中找到对应的实际意义。
