算法笔记——树

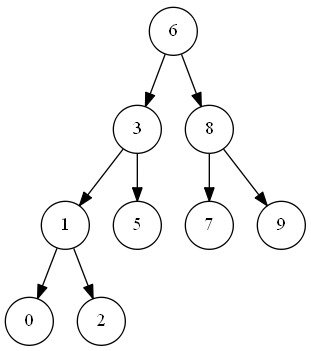
二叉搜索树中的插入操作：Given the root node of a binary search tree (BST) and a value to be inserted into the tree, insert the value into the BST. Return the root node of the BST after the insertion. It is guaranteed that the new value does not exist in the original BST. 链接
二叉搜索树的范围和：Given the root node of a binary search tree, return the sum of values of all nodes with value between L and R (inclusive). 链接
二叉搜索树中第K小的元素：Given a binary search tree, write a function kthSmallest to find the kth smallest element in it. 链接

上面3题中，第一题是BST的插入问题，后两题是BST的搜索问题。

插入的算法可以用递归来完成，这里的插入还算简单，不需要对树的其他节点做调整，参考代码：

def insertIntoBST(self, root, val):
    if root.val > val:
        if not root.left:
            root.left = TreeNode(val)
        else:
            self.insertIntoBST(root.left, val)
    else:
        if not root.right:
            root.right = TreeNode(val)
        else:
            self.insertIntoBST(root.right, val)
    return root

二叉搜索树的范围和，也就是需要找出所有在二叉树中指定区间范围内的值。可以使用深度遍历或者广度遍历。下面的是广度遍历的参考代码：

def rangeSumBST(self, root, L, R):
    ans = 0
    stack = [root]
    while stack:
        node = stack.pop()
        if node:
            if L <= node.val <= R:
                ans += node.val
            if L < node.val:
                stack.append(node.left)
            if node.val < R:
                stack.append(node.right)
    return ans

对于寻找二叉搜索树中第K小的元素，需要用到中序遍历，将在下面提到。

红黑树

红黑树本质上是一棵二叉搜索树，但它在二叉搜索树的基础上增加了着色和相关的性质使得红黑树相对平衡，从而保证了红黑树的查找、插入、删除的时间复杂度最坏为 $O(logn)$ 。

红黑树的特性：

每个节点或者是黑色，或者是红色。
根节点是黑色。
每个叶子节点（NIL）是黑色。【注意：这里叶子节点，是指为空(NIL或NULL)的叶子节点！】
如果一个节点是红色的，则它的子节点必须是黑色的。
从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。

红黑树的左右旋是比较重要的操作，左右旋的目的是调整红黑节点结构，转移黑色节点位置，使其在进行插入、删除后仍能保持红黑树的 5 条性质。

红黑树的增删操作比较复杂，在此就不多说了。看下面这个问题。

区间和的个数：Given an integer array nums, return the number of range sums that lie in [lower, upper] inclusive. Range sum S(i, j) is defined as the sum of the elements in nums between indices i and j (i ≤ j), inclusive. 链接

在考虑这条题目之前，先来看看“计算右侧小于当前元素的个数”这个题目。给定一个数组，统计每个数的右侧，有多少个小于当前数值的元素。接解题的思路是，从右往左遍历，在遍历的同时，构建一颗二叉搜索树。每当需要在二叉搜索树中插入元素时，就可以顺便统计一下有多少节点小于当前值，也就是在数组中当前元素的右侧有多少个数小于当前值。

回到这条题目：在给定数组中，求区间和满足指定范围的的区间的个数。可以简单的双重循环一遍，但是这样效率很差。结合“”题目来看，事先计算好数组的求和结果可以提高一些效率，定义新的数组 T，令 $Ti =$ 。题目中想要求的区间实际上就是，区间 $(i,j)$ 的和等于。

问题就转换为了：对于每一个位置，在它的右侧有多少个元素满足“与当前位置的差在指定的区间范围内”。所以，解法参照上面的题目，从右往左遍历，一边遍历一边构造二叉树，从而解决题目中的问题。考虑到输入的数组的大小，红黑树可能比二叉搜索树更加合适。

霍夫曼树

霍夫曼树又称最优二叉树，是一种带权路径长度最短的二叉树。霍夫曼编码是哈夫曼树的一个应用，霍夫曼编码使用变长编码表对源符号（如文件中的一个字母）进行编码，其中变长编码表是通过一种评估来源符号出现几率的方法得到的，出现几率高的字母使用较短的编码，反之出现几率低的则使用较长的编码，这便使编码之后的字符串的平均长度、期望值降低，从而达到无损压缩数据的目的。

霍夫曼树的构建过程可参考此文章。LeetCode上关于霍夫曼树的问题不多，下面是我找到的其中一条：

建造街区的最短时间：You are given a list of blocks, where blocks[i] = t means that the i-th block needs t units of time to be built. A block can only be built by exactly one worker. A worker can either split into two workers (number of workers increases by one) or build a block then go home. Both decisions cost some time. The time cost of spliting one worker into two workers is given as an integer split. Note that if two workers split at the same time, they split in parallel so the cost would be split. Output the minimum time needed to build all blocks. 链接

这个问题和霍夫曼树有什么关联呢？如果一个街区需要更多的时间来建造，也就对应着出现几率高的字母，得到的编码就越短，在工期的安排上就越优先。在建造工期长的街区的同时，另一个工人可以把时间花在招工，并完成工期短的街区。具体的构建过程，以输入参数 blocks [1, 2, 4, 7, 10]，split cost 3 为例：

对街区工期进行排序，先分析前两个：

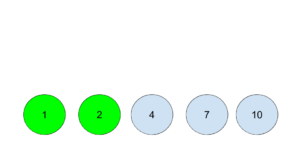
对于前两个街区，需要花费的时间是，先花3天时间招个工，2个工人分别建造街区，时间花费max(1,2)天，共计split+max(1,2)，也就是5天。其余的依此类推。

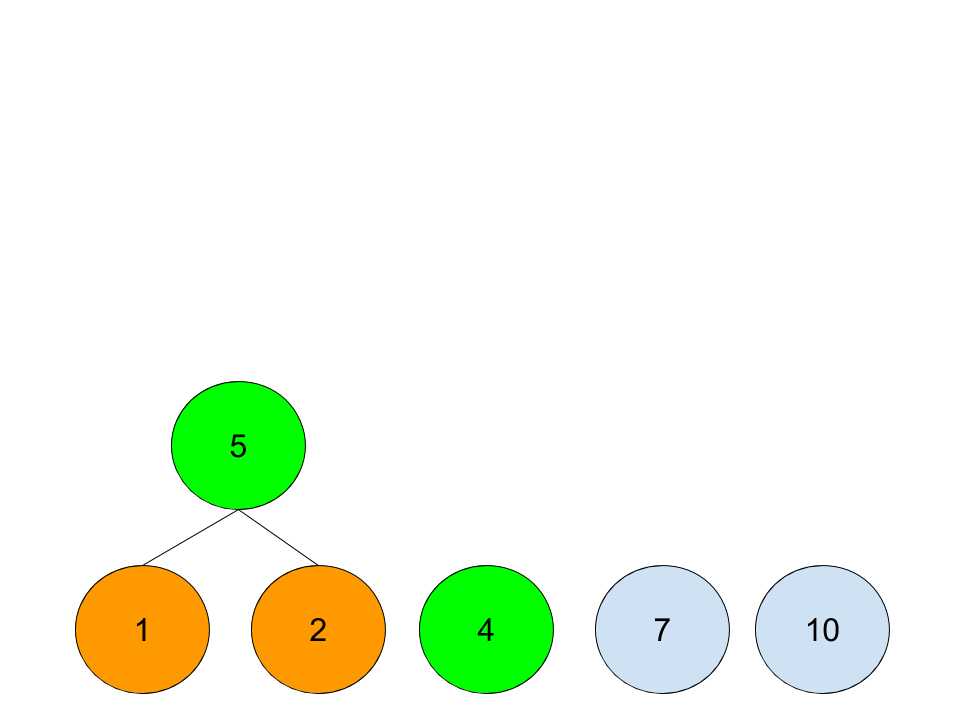
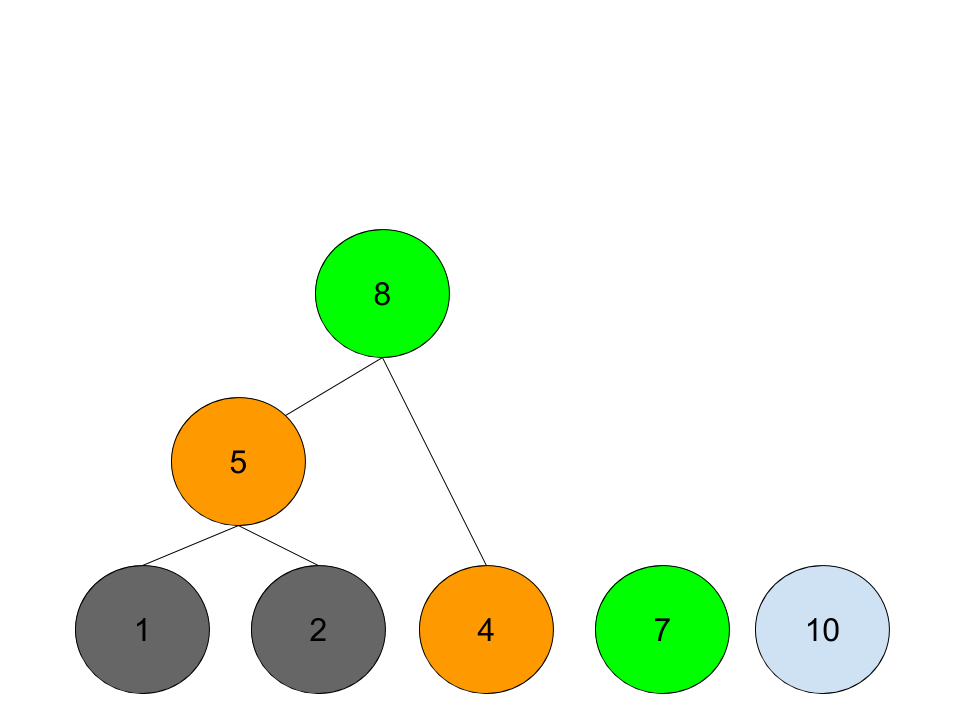
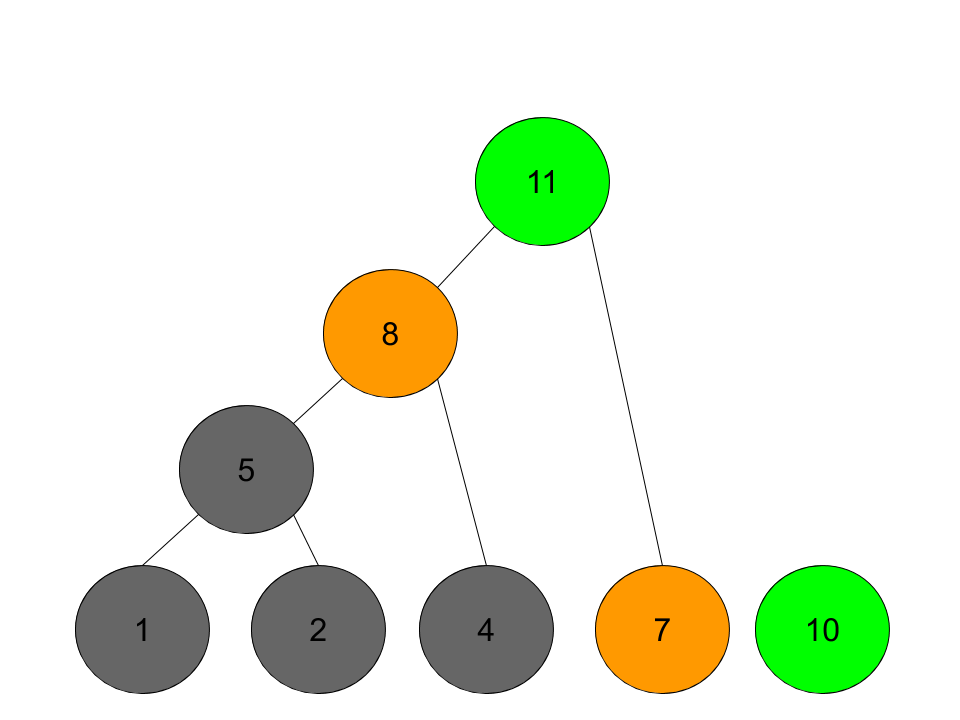
最终，一个霍夫曼树就算构建完成了，生成的过程是自底向上的，实际的执行过程是自顶向下的，也就是：第一个工人先花3天招一个新工人，让他去建造需要花10天的街区；同时，第一个工人再花3天招一个新工人，让他去建造需要花7天的街区；依此类推。直到最后一个需要花1天的街区，就自己上了。

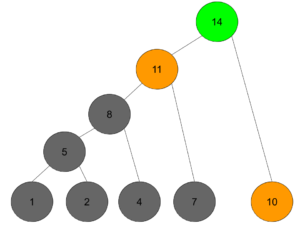
剩下的就代码实现了，参考代码：

def minBuildTime(self, blocks, split):
    heapq.heapify(blocks)
    while True:
        if len(blocks) == 1:
            return blocks[0]
        a, b = heapq.heappop(blocks), heapq.heappop(blocks)
        # as b is great or eqaul to a, so no need to max(a,b) + split
        heapq.heappush(blocks, b+split)

树的搜索及遍历

广度优先遍历和深度优先遍历

广度优先遍历

从根节点开始，沿着树的宽度遍历树的节点。如果所有节点均被访问，则算法中止。

当问题的解对应着一颗树的层数，或者需要在同层的节点中寻找答案的时候，广度优先遍历可能是一个不错的选择。

二叉树的锯齿形层次遍历：Given a binary tree, return the zigzag level order traversal of its nodes’ values. (ie, from left to right, then right to left for the next level and alternate between). 链接
对称树：Given a binary tree, check whether it is a mirror of itself (ie, symmetric around its center). 链接
二叉树的最小深度：Given a binary tree, find its minimum depth. 链接

上面的问题中，前2个问题是以树的每一层为单位进行的，第1题需要输出树的每一层，并根据行数进行反转。第2题需要判断树的每一层是否是对称。第3个问题需要广度优先遍历这棵树，直到出现空节点。

二叉树的最小深度的广度优先遍历的参考代码：

def minDepth(self, root):
    if not root:
        return 0
    
    node_list = [root]
    depth = 1
    
    while node_list:
        temp = []
        for node in node_list:
            if not node.left and not node.right:
                return depth
            if node.left:
                temp.append(node.left)
            if node.right:
                temp.append(node.right)
        depth += 1
        node_list = temp

当然，递归也是一个不错的选择：

def minDepth(self, root: TreeNode) -> int:
    if root is None:
        return 0
    if root.left is None and root.right is None:
        return 1
    if not root.left:
        return 1 + self.minDepth(root.right)
    if not root.right:
        return 1 + self.minDepth(root.left)
    return 1 + min(self.minDepth(root.left), self.minDepth(root.right))

深度优先遍历

沿着树的子节点遍历树，尽可能深的搜索树的分支。当节点v的所有子节点都己被探寻过，搜索将回溯到节点v的父节点。这一过程一直进行到已发现所有节点为止。

相比广度优先遍历，深度优先遍历能够很方便的获取一条路径上的前后节点，因此适用性更广一些。深度优先遍历常常以递归的形式来实现。

路径之和：Given a binary tree and a sum, find all root-to-leaf paths where each path’s sum equals the given sum. 链接
二叉树的最近公共祖先：Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree. 链接

第一题路径之和需要判断一条从根节点到叶子节点的路径之和是否等于给定值。如果使用广度优先遍历就需要在遍历过程中将整颗树的路径都保存下来，会占用很大的空间。第二题需要寻找2个子节点的最近公共祖先。采用递归，判断当前节点的左右子树是否包含给定的节点，如果左子树包含且右子树也包含，则当前节点为最近公共祖先。参考代码：

def lowestCommonAncestor(self, root, p, q):
    if not root: return None
    if p == root or q == root:
        return root
    left = self.lowestCommonAncestor(root.left, p , q)
    right = self.lowestCommonAncestor(root.right, p , q)
        
    if left and right:
        return root
    if not left:
        return right
    if not right:
        return left

两者比较

广度优先遍历一般需要存储产生的所有结点，占的存储空间要比深度优先遍历大得多，因此程序设计中，必须考虑溢出和节省内存空间得问题。

感觉没有什么问题是只能用广度优先遍历或者深度优先遍历来解，无非是一种更方便一点，另外一种在编码难度和效率上略逊一点。

N叉树的最大深度：Given a n-ary tree, find its maximum depth. 链接
求根到叶子节点数字之和：Given a binary tree containing digits from 0-9 only, each root-to-leaf path could represent a number. An example is the root-to-leaf path 1->2->3 which represents the number 123. Find the total sum of all root-to-leaf numbers. 链接
删除无效的括号：Remove the minimum number of invalid parentheses in order to make the input string valid. Return all possible results. 链接

上面的题目既可以用广度优先遍历来实现，也可以用深度优先遍历来实现。

第一题N叉树的最大深度可以使用广度优先遍历，统计总共遍历了几层。也可以使用深度优先遍历，计算各个从根节点到叶子节点的路径的长度，取最大值。

第二题使用两种遍历方法的解题思路与第一题类似。

第三题删除无效括号，因为可能存在多组解，所以需要将所有的结果输出。用深度优先遍历或者广度优先遍历均可。下面分别是通过不同的遍历方法来求解：

def removeInvalidParentheses(self, s):
    def dfs(s):
        mi = calc(s)
        if mi == 0:
            return [s]
        ans = []
        for x in range(len(s)):
            if s[x] in ('(', ')'):
                ns = s[:x] + s[x+1:]
                if ns not in visited and calc(ns) < mi:
                    visited.add(ns)
                    ans.extend(dfs(ns))
        return ans
        
    def calc(s):
        a = b = 0
        for c in s:
            a += {'(' : 1, ')' : -1}.get(c, 0)
            b += a < 0
            a = max(a, 0)
        return a + b

    visited = set([s])    
    return dfs(s)

def removeInvalidParentheses(self, s):
    def isvalid(s):
        ctr = 0
        for c in s:
            if c == '(':
                ctr += 1
            elif c == ')':
                ctr -= 1
                if ctr < 0:
                    return False
        return ctr == 0
    level = {s}
    while True:
        valid = filter(isvalid, level)
        if valid:
            return valid
        level = {s[:i] + s[i+1:] for s in level for i in range(len(s))}

二叉树的遍历

二叉树还存在着一些独特的遍历手段：

前序遍历：Given a binary tree, return the preorder traversal of its nodes’ values. 链接
中序遍历：Given a binary tree, return the inorder traversal of its nodes’ values. 链接
后序遍历：Given a binary tree, return the postorder traversal of its nodes’ values. 链接

以及一些围绕这三种遍历方式的问题：

根据前序遍历和后序遍历构建二叉树：Return any binary tree that matches the given preorder and postorder traversals. 链接
N叉树的前序遍历：Given an n-ary tree, return the preorder traversal of its nodes’ values. 链接
二叉搜索树中第K小的元素：Given a binary search tree, write a function kthSmallest to find the kth smallest element in it. 链接

第一，二题比较简单。对于第三题，可以根据二叉搜索树的特性进行中序遍历，因为二叉搜索树的中序遍历即为二叉搜索树的所有节点的排序结果，所以再中序遍历时，得到的第K个结果即为题解。参考代码：

def kthSmallest(self, root, k):
    i=0
    stack=[]
    node=root
    while node or stack:
        while node:
            stack.append(node)
            node=node.left
        node=stack.pop()
        i+=1
        if i==k:
            return node.val
        node=node.right

其他问题

树转图

如果在使用树的过程中，频繁的需要根据子节点获取父节点时，一种做法是为每个子节点添加一个父节点属性，或者干脆就将树转换为无向图来处理。参考问题：

冗余连接：The given input is a graph that started as a tree with N nodes (with distinct values 1, 2, …, N), with one additional edge added. The added edge has two different vertices chosen from 1 to N, and was not an edge that already existed. Return an edge that can be removed so that the resulting graph is a tree of N nodes. 链接
二叉树中所有距离为 K 的结点：We are given a binary tree (with root node root), a target node, and an integer value K. Return a list of the values of all nodes that have a distance K from the target node. The answer can be returned in any order. 链接

具体解法在《算法笔记——图》中详细介绍。

动态规划

因为树本身的数据结构的限制，一方面，我们得到的是顶点，而不是叶子节点的集合；另一方面，基本的树结构只能从父节点获取子节点，而不能从子节点得到父节点。

这两个特点决定了树状的动态规划问题自底向上的求解是比较困难的，进而就投向了深度遍历的怀抱。或者说是“记忆化搜索”。参考问题：

不同的二叉搜索树：Given n, how many structurally unique BST’s (binary search trees) that store values 1 … n ? 链接
打家劫舍 III：The thief has found himself a new place for his thievery again. There is only one entrance to this area, called the “root.” Besides the root, each house has one and only one parent house. After a tour, the smart thief realized that “all houses in this place forms a binary tree”. It will automatically contact the police if two directly-linked houses were broken into on the same night. Determine the maximum amount of money the thief can rob tonight without alerting the police. 链接
二叉树布控：Given a binary tree, we install cameras on the nodes of the tree. Each camera at a node can monitor its parent, itself, and its immediate children. Calculate the minimum number of cameras needed to monitor all nodes of the tree. 链接

具体解法在《算法笔记——动态规划》中详细介绍。

简介

常见应用场景

不同类型的树

二叉搜索树

红黑树