实现克里金(kriging)插值（一）计算原理

这篇文章是大三的一个课程大作业，最初发布在 CSDN 上。因为当时花了很多精力在这上面，所以决定搬过来。

克里金插值较为复杂，但效果也是比较好的。为了能够通过代码实现克里金插值的过程，首先需要了解其详细的计算过程。

---

在ArcGIS中实现克里金插值计算

导入散点数据

在“Geostatistical Analyst”中选择“地统计向导”。找不到的先右击菜单栏空白处，勾选“Geostatistical Analyst”。

选择数据

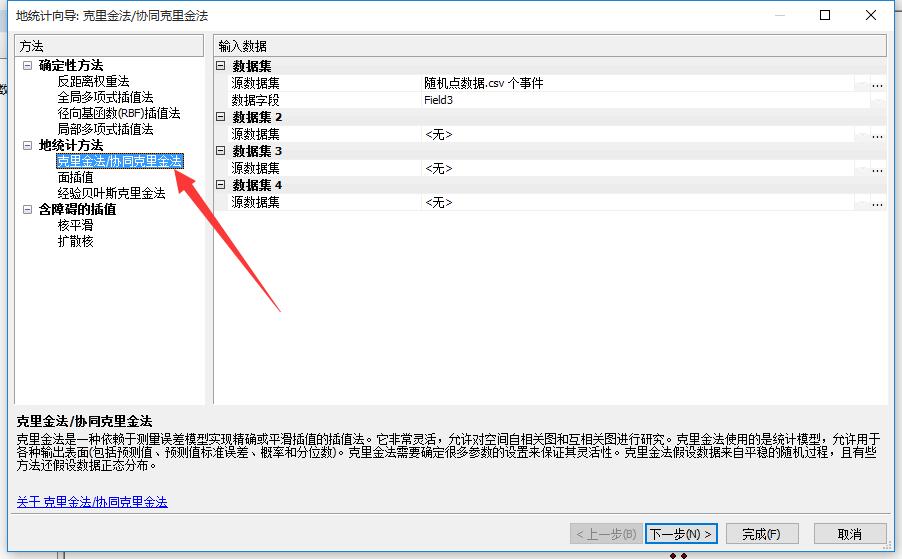
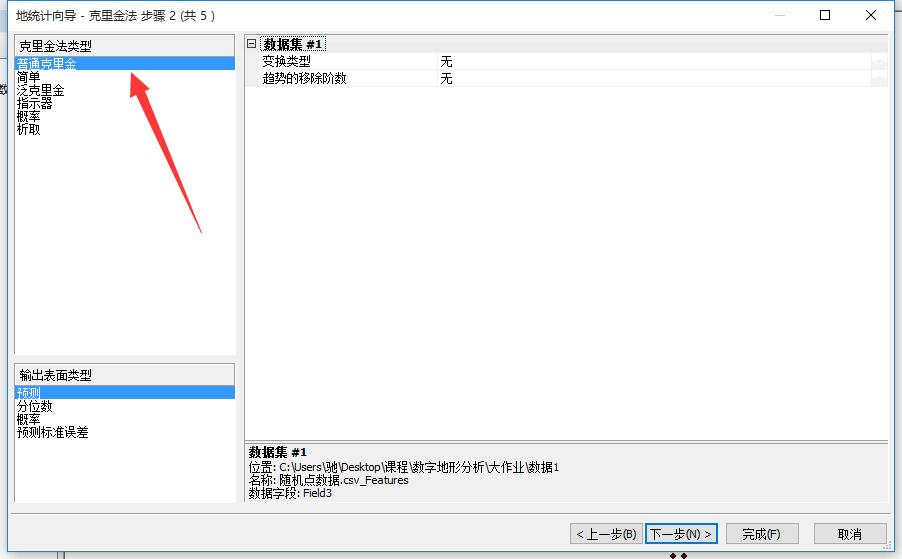
选择“普通克里金”

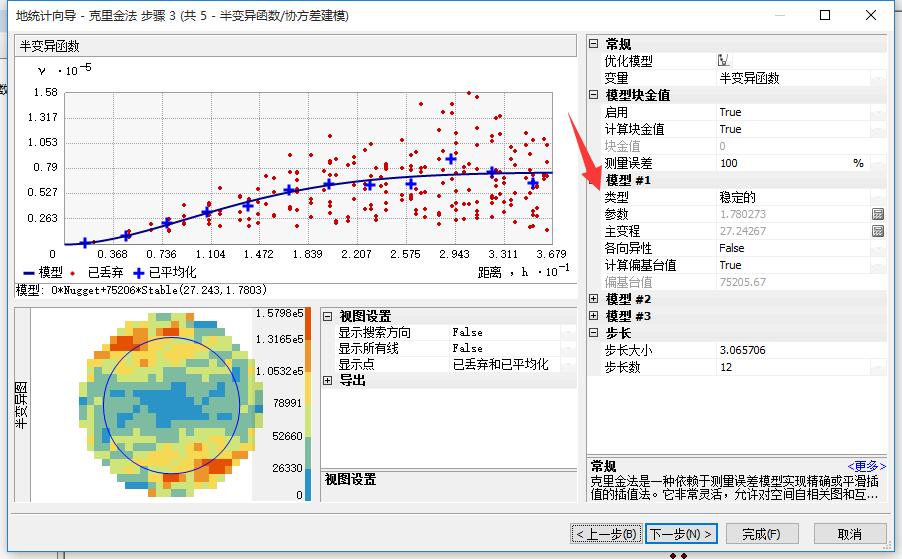
拟合界面

这个界面的内容很重要，也正是帮助文档中所解释的内容。左上角的拟合曲线是我们将要在C#代码中实现的，坐标系中的散点也是需要我们去通过计算得到的。

查看拟合函数类型

点开上图界面中的“类型”，可以看到如下的几种：球面函数，指数函数，高斯函数等。选择其中不同的类型，左侧的拟合曲线也会相应的改变，这几种函数在帮助文档中有介绍到。

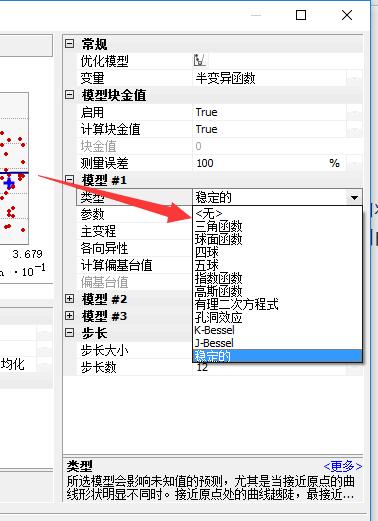
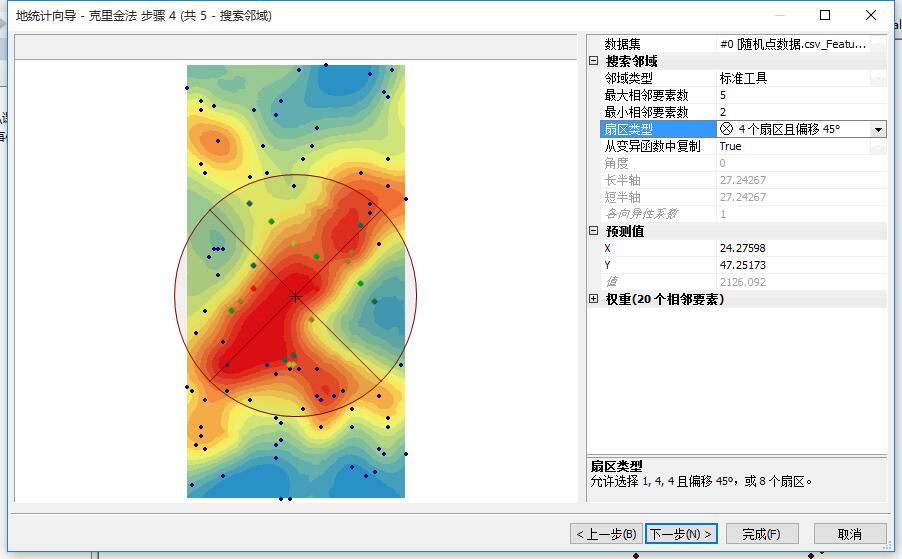
查看插值的结果

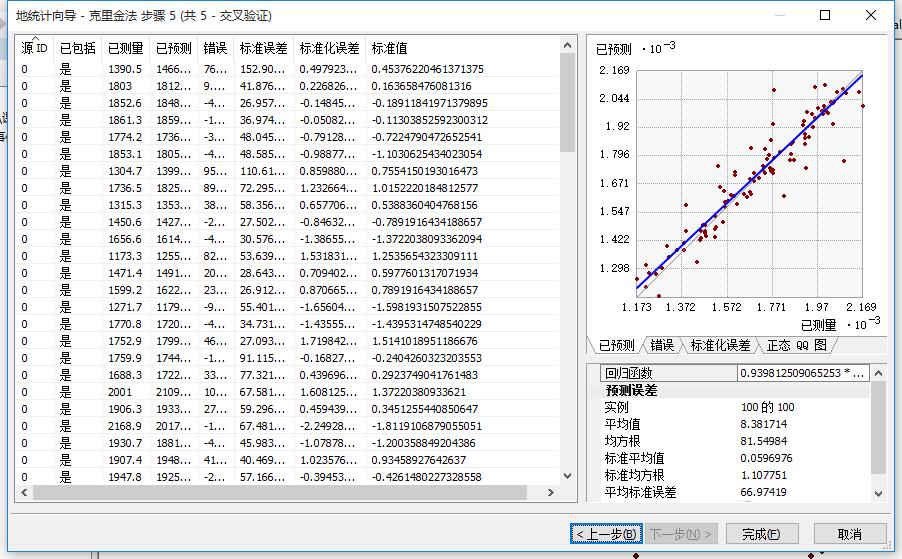
误差分析的界面

---

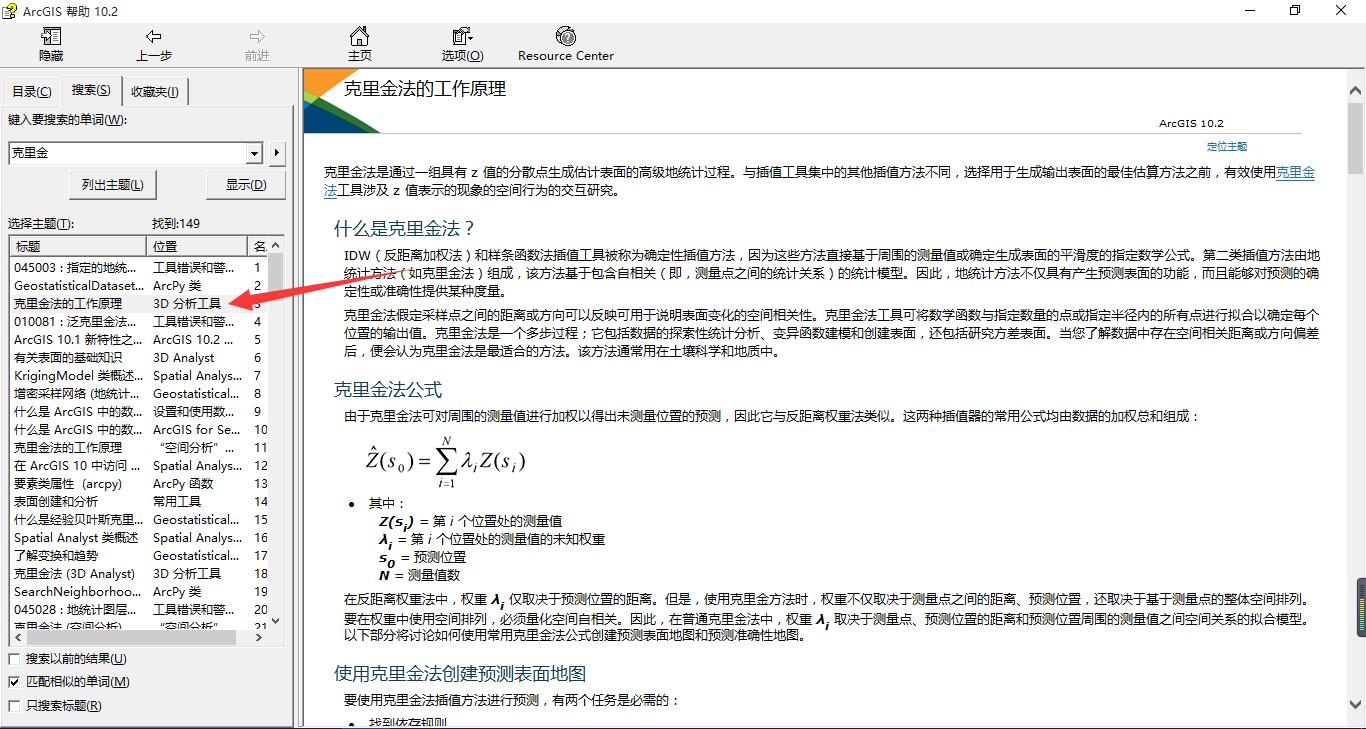
阅读ArcGIS中的有关克里金插值的文档

打开ArcGIS的帮助文档，搜索“克里金”，选择“克里金法的工作原理”。

求取散点的半方差

公式：
其中就是指，两点的距离，也就是坐标中的X轴的变量，计算得到的就是坐标轴中Y轴的变量。

如果有100个点，每个点都与其他的99个点计算半方差，但是这样会产生大量的数据，而且这些数据中有一部分是重复的。这样执行拟合的效率也会很低。按照帮助文档的说法，我们要精简得到的结果。比如：0~10之间的点求一个均值，10~20，20~30……

这样，我们就可以得到多个坐标点，如图，红色的点就是初始求得的点，蓝色的点就是均值点：

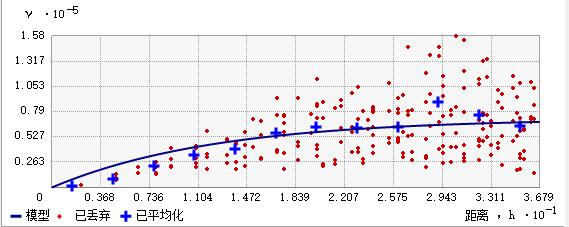
拟合坐标点，求取主变程和基台值

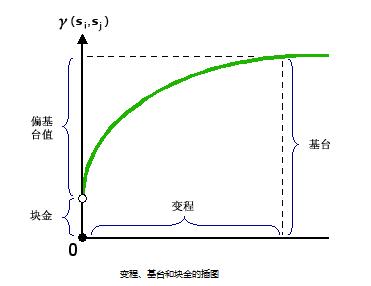
拟合主要是针对蓝色的点，拟合函数有多种选择，函数中的是块金值，是偏基台值，或是主变程值，块金值在拟合中一般默认为0。

球形模型

指数模型

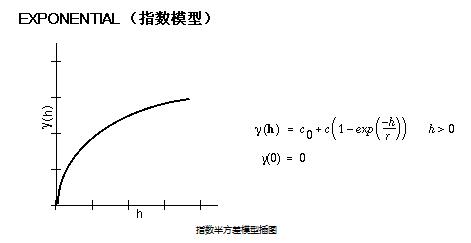
高斯模型

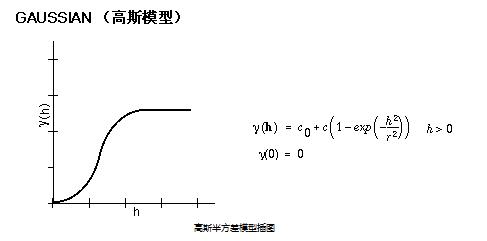
在以上三个模型中，抛开默认为0，球形模型的方程有3个未知量，高斯模型和指数模型有2个未知量，因为需要用C#程序去实现这个拟合的过程，我选择了较为简单的指数模型，其公式为：

   

通过拟合得到，，得到了半方差的插值模型，我们就可以进行下一步的插值计算了。

求取未知点的插值结果

接下来的插值计算过程帮助文档中未详细描述，我从一次比赛的pdf中得到了计算过程，在此分享一下。
设函数为上面所求得的模型，为，两点之间的距离。

设，用于计算矩阵，向量。矩阵K是用已知散点求得的，表达式如下：

   

向量是计算当前要求的未知点与已知点之间的，公式如下：

   

利用矩阵和向量，能够求得向量，表示第个已知点对当前未知点的影响权重，公式：

计算点的高程值得公式如下，其中表示点的高程值：

这样，一个未知点的高程值就预测出来了，矩阵针对同一批散点是确定的。所以，预测其他坐标的高程值时，只需要重复计算向量。